Integrated Rate Equation

View Assign Share Link Report

Integrated Rate Equation

This lesson aligns with NGSS PS1.B

Introduction

Chemical reactions can be complex, involving multiple steps and intermediate species. To describe the rate of a reaction, scientists use the concept of reaction rate, which represents the change in concentration of reactants or products per unit time. The rate of a reaction is often expressed as the change in concentration of a particular species over time. In this article, we will delve into the concept of integrated rate equations, their significance, and how they contribute to our understanding of reaction kinetics.

Why do we need the Integrated Rate Equation?

A mathematical expression that illustrates the relationship between the rate of a reaction and the concentration of the reacting species is referred to as a differential rate equation. The instantaneous rate of reaction is defined as the slope of the tangent at any given moment on the concentration-time graph. However, determining the rate of reaction directly from the concentration-time graph can be challenging due to its complex nature.

To address this challenge, the differential rate equation is integrated to establish a connection between the concentration at various points and the rate constant. This resultant equation is commonly known as the integrated rate equation.

Integrated Rate Equations

Integrated rate equations are mathematical expressions that relate the concentrations of reactants or products to time. These equations are derived by integrating the differential rate law, which describes the rate of a reaction at a specific moment. The integration process simplifies the rate law and allows chemists to analyze the concentration changes throughout the entire course of a reaction.

There are various types of integrated rate equations, and their form depends on the order of the reaction. The order of a reaction with respect to a particular reactant is the exponent to which its concentration is raised in the rate law.

Let's explore the integrated rate equations for different reaction orders:

Zero-Order Reactions

In a zero-order reaction, the rate is independent of the concentration of the reactant. Examples of zero-order reactions are rarely observed. Examples illustrating zero-order reactions include the thermal decomposition of HI on a gold surface and the decomposition of gaseous ammonia on a hot platinum surface.

A → B

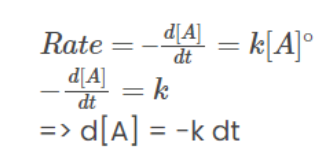
Integrating on both sides:

⇒ [A] = -kt + c………………………..(1)

Where,

c= constant of integration,

At time, t=0,[A] =[math][A]_0[/math]

Putting this value in equation (1) we get the value of c,

[math][A]_0[/math] = c

The integrated rate equation for a zero-order reaction is given by:

[A]=−kt+[math][A]_0[/math]

where:

[A] is the concentration of the reactant at time t,
k is the rate constant,
t is time, and
[math][A]_0[/math] is the initial concentration of the reactant.

This equation suggests that in a zero-order reaction, the concentration of the reactant decreases linearly with time.

First-Order Reactions:

For a first-order reaction, the rate is directly proportional to the concentration of the reactant. Examples illustrating first-order reactions include the natural and artificial radioactive decay of unstable nuclei. A generalized equation for a first-order reaction, expressed with the rate constantk, is derived as follows:

A → B

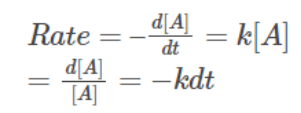
Integrating on both sides:

=> ln [A] = -kt + c……………………….(2)

Where,

c= constant of integration,

At time, t=0,

[A] =[math][A]_0[/math]

Putting this value in equation (2) we get the value of c,

[math][A]_0[/math] = c

The integrated rate equation is:

ln[A]=−kt+ln[math][A]_0[/math]

where:

ln[A] is the natural logarithm of the concentration of the reactant at time t.
In a first-order reaction, the natural logarithm of the concentration of the reactants decreases linearly with time.

We can also find the value of the rate constant, k from the equation as:

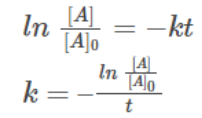
Concentration at any instant of time can be given as,

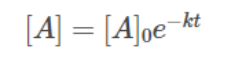
Hence, utilizing an integrated rate equation for zero and first-order reactions enables the determination of both the concentration and rate of reaction at any given moment.

Second-Order Reactions:

In a second-order reaction, the rate is proportional to the square of the concentration of the reactant. The integrated rate equation is:

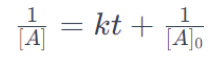
where:

1/[A] represents the reciprocal of the concentration of the reactant at time t.In a second-order reaction, the reciprocal of the concentration is linearly related to time.

Significance of Integrated Rate Equations:

Determining Reaction Order:

Integrated rate equations allow chemists to experimentally determine the order of a reaction by monitoring concentration changes over time. By comparing the experimental data with the integrated rate equations, the reaction order can be identified.

Predicting Concentrations and Rate Constants at Specific Times:

Integrated rate equations enable the prediction of reactant or product concentrations as well as the rate constants at specific time points during a reaction.

Understanding Reaction Mechanisms:

Integrated rate equations provide insights into the reaction mechanisms by revealing how the concentrations of reactants and products change over time.

Summary

Integrated rate equations are mathematical expressions that relate the concentrations of reactants or products to time.
These equations are derived by integrating the differential rate law, which describes the rate of a reaction at a specific moment.
In a zero-order reaction, the rate is independent of the concentration of the reactant.
For a first-order reaction, the rate is directly proportional to the concentration of the reactant.

Related Worksheets: