Rate Constant and Half Life
Rate Constant and Half Life
This lesson aligns with NGSS PS1.B
Introduction
Chemical kinetics investigates the speed at which chemical reactions occur and the factors influencing their rates. Two key concepts in chemical kinetics are rate constants and half-life. The term "rate constant" refers to the constant that establishes the connection between the molar concentration of reactants and the pace at which a chemical reaction progresses. This important parameter is denoted by the symbol "k." In this article, we will delve into the definitions of rate constants and half-life, exploring their definitions, mathematical expressions, and their significance.
Rate Constants
The rate constant, often denoted as k, represents the proportionality constant in the rate equation that relates the rate of reaction to the concentrations of reactants. The general form of a first-order reaction rate equation is given by:
Rate=k[A]
Here,[A] is the concentration of the reactant, and
k is the rate constant.
The units of k depend on the overall reaction order, and for a first-order reaction, it is typically expressed in units of reciprocal time (e.g., s⁻¹).For a more complex reaction with multiple reactants, the rate equation might take the form:
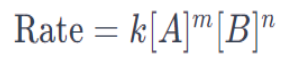
m and n represent the respective reaction orders for reactants A and B.
Half-Life
The duration required for half of a set of reactions to conclude, or the point at which the concentration of the reactant diminishes to fifty percent of its initial value, is referred to as the half-life period of the reaction.
The half-life is typically represented by the symbol [math]t_1/2[/math]. The concept of half-life is frequently employed in nuclear physics to characterize radioactive decay or the longevity of stable atoms. Initially introduced by Ernest Rutherford for the analysis of rock age determination. The determination of half-life values depends upon the reaction's order.
The concept of half-life is commonly associated with radioactivity, but it extends to chemical kinetics and reactions as well. The half-life ([math]t_1/2[/math]) is the time required for the concentration of a reactant to decrease to half of its initial value.
Half-Life for Zero-Order Reaction
A zero order reaction indicates that the rate of the reaction does not depend on the concentration of the reactant. For a general reaction;
A → Product
The rate law of zero order kinetics is: [math][A]_0[/math] = [A] + kt
Where
[math][A]_0[/math] = Initial concentration of reactant at time(t) = 0
[A] = concentration of reactant at time (t) = t
When time(t) = [math]t_1/2[/math]
the concentration of the reaction
From the rate law of zero order kinetics is:
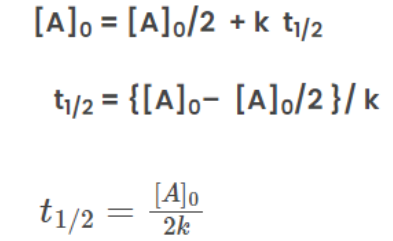
Half-Life for First Order Reaction
For a general reaction;
A → Product
The rate law of zero order kinetics is:
ln [math][A]_0[/math] = ln [A] + k t
Where [math][A]_0[/math]= Initial concentration of reactant at time(t) = 0
[A] = concentration of reactant at time (t) = t
When time(t) = [math]t_1/2[/math] ,
the concentration of the reaction([A]) = [math][A]_0[/math]/2
From the rate law of zero order kinetics is:
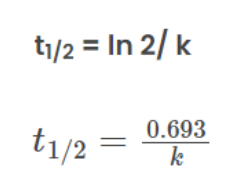
This formula implies that the half-life is inversely proportional to the rate constant. As the rate constant increases, the half-life decreases, signifying a faster reaction.
Half-Life for Second Order Reaction
For a general reaction;
2A → Product
The rate law of zero order kinetics is:
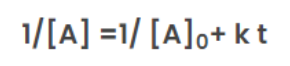
Where [math][A]_0[/math] = Initial concentration of reactant at time(t) = 0
[A] = concentration of reactant at time (t) = t
When time(t) = [math]t_1/2[/math] ,
the concentration of the reaction([A]) = [math][A]_0[/math]/2
From the rate law of zero order kinetics is:
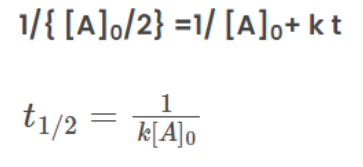
Half-Life for nth Order Reaction
For a general reaction;
nA → Product
The rate law of zero order kinetics is:
Where [math][A]_0[/math]= Initial concentration of reactant at time(t) = 0
[A] = concentration of reactant at time (t) = t
When time(t) = [math]t_1/2[/math] ,
the concentration of the reaction([A]) = [math][A]_0[/math]/2
Half life formula of nth order reaction is:
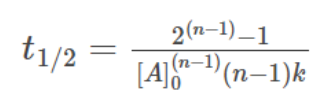
Significance of Half-Life:
Understanding the half-life of a reaction provides crucial insights into its kinetics and temporal behavior. Key points of significance include:
Reaction Monitoring:
The half-life serves as a valuable tool for monitoring reaction progress. Researchers can assess how quickly a reactant is being consumed or a product is being formed.
Stability of Compounds:
In pharmaceuticals and chemical engineering, knowledge of the half-life is essential for determining the stability of compounds over time. This is particularly relevant in drug formulation and shelf-life assessment.
Radioactive Decay:
In nuclear chemistry, half-life is synonymous with the time required for half of a radioactive substance to decay. This parameter is crucial for radiometric dating and understanding the behavior of radioactive isotopes.
Reaction Optimization:
In industrial processes, optimising reaction conditions often involves considering the half-life. Minimising the half-life can lead to increased efficiency and reduced processing times.
Summary
- The rate constant represents the proportionality constant in the rate equation that relates the rate of reaction to the concentrations of reactants.
- The point at which the concentration of the reactant diminishes to fifty percent of its initial value, is referred to as the half-life period of the reaction.
- The half-life is typically represented by the symbol [math]t_1/2[/math].
Related Worksheets:
Become a Help Teaching Pro subscriber to access premium lessons
Unlimited premium lessons Unlimited premium printables Unlimited online testing
- Already a Pro subscriber? Log in for access
- Browse free lessons
- Go back to previous page