Mass Defect and Nuclear Binding Energy
Mass Defect and Nuclear Binding Energy
This lesson aligns with NGSS PS1.C
Introduction
In the 20th century, the renowned Albert Einstein introduced the groundbreaking theory known as "the theory of relativity." This theory revealed the interconvertibility of mass and energy – the idea that mass can be transformed into energy and vice versa. This new insight in physics played a crucial role in resolving numerous problems and provided a platform for the development of various new theories. One such theory that emerged from this conceptual shift is the concept of Nuclear Binding Energy, which offers a distinct perspective on nuclear mass and interactions between atomic nuclei. In this article, we will learn about mass defect, nuclear binding energy, and how binding energy is calculated.
Mass Defect:
An atom is structured with a central nucleus surrounded by electrons in an orbital manner. The nuclei are composed of protons and neutrons, collectively referred to as nucleons. One might anticipate that the mass of the nucleus would equal the sum of the individual masses of protons and neutrons. However, this assumption is incorrect. The actual total mass of the nucleus (mNuc) is found to be less than the sum of the individual masses of neutrons and protons, the very constituents that make up the nucleus.
The mass defect is a measure of the difference between the mass of an atomic nucleus and the sum of the masses of its individual protons and neutrons. This discrepancy arises due to the conversion of mass into energy during the formation of the nucleus, in accordance with Einstein's famous equation, E=mc². Essentially, the mass defect represents the "missing" mass that has been converted into binding energy to hold the nucleus together.
The relationship between mass defect (Δm) and nuclear binding energy (BE) can be expressed using the formula:
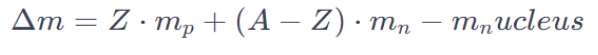
Where:
- Z is the number of protons (atomic number)
- A is the mass number (sum of protons and neutrons)
- mp is the mass of a proton
- mn is the mass of a neutron, and
- mNuc is the actual measured mass of the nucleus.
The mass defect is crucial in determining the amount of energy released or absorbed during nuclear reactions, serving as a fundamental parameter in the calculation of nuclear binding energy.
Nuclear Binding Energy:
Nuclear binding energy is the energy required to disassemble a nucleus into its individual protons and neutrons. This energy is a direct consequence of the mass defect and is intimately connected to the stability of the nucleus.
The formula to calculate nuclear binding energy (BE) from the mass defect (Δm) is given by:
BE=Δm⋅c2
Where:
c is the speed of light (3.00×108 m/s)
How to Calculate Nuclear Binding Energy
The calculations of nuclear binding energy involves the following steps:
- After determining the mass defect, the nuclear binding energy can be calculated by converting that mass into energy using the formula
- Ensure that the mass is expressed in kilograms (kg).
- Once the energy value is obtained, it can be normalized into per-nucleon and per-mole quantities for further analysis.
Binding Energy Calculations for Deuteron:
Mass of deuteron mD = 1875.61MeV/c2 or 3.34359✕10-27 Kg.
Atomic Mass number of Deuteron; A=2
The atomic number of Deuteron; Z=1
Mass defect Δm =?
Binding energy B.E= ?
Solution:
Mass defect can be calculated by:
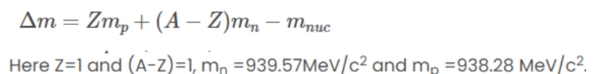
Substituting the values we get:

=2.24 MeV/c2
Thus, the mass defect is 2.24 MeV/c2
Binding Energy can be calculated by:
BE=Δm⋅c2
=2.24 MeV
A minimum energy of 2.24 million electron volts is essential to break a Deuteron into a Proton and Neutron. This energy requirement is notably high. In contrast, the energy needed to detach an electron from a hydrogen atom, surpassing the electromagnetic force (Coulomb force), is approximately 10 electron volts. Drawing this comparison distinctly indicates the strength of the nuclear force.
Despite its effective range being in the order of multiple femtometers, the nuclear force stands out as one of the strongest force in the natural world.
Summary
- The mass defect is a measure of the difference between the mass of an atomic nucleus and the sum of the masses of its individual protons and neutrons.
- Nuclear binding energy is the energy required to disassemble a nucleus into its individual protons and neutrons.
- A minimum energy of 2.24 million electron volts is essential to break a Deuteron into a Proton and Neutron. This energy requirement is notably high.
Related Worksheets:













