Newton's Second Law of Motion

View Assign Share Link Report

Newton's Second Law of Motion

This lesson aligns with NGSS PS2.A

Introduction

Newton's laws of motion are fundamental principles that elucidate the behavior of objects in response to forces. Sir Isaac Newton, in his seminal work "Philosophiæ Naturalis Principia Mathematica," introduced these laws, providing a framework for comprehending motion. Newton's second law of motion, a key component of classical mechanics, delves into the relationship between force, mass, and acceleration. In this educational article, we will explore Newton's second law, elucidate its principles, and work through examples and problems to deepen our understanding.

Newton's Second Law of Motion

The relationship between force and momentum can be expressed as the force being equal to the rate of change of momentum. In the case of a constant mass, force is equivalent to the product of mass and acceleration.

Newton's second law states that the acceleration of an object is dependent on two factors: the net force acting upon the object and the mass of the object. The acceleration of the body is directly linked to the net force applied to it and exhibits an inverse relationship with its mass.

In simpler terms, an increase in the applied force results in a proportional increase in the object's acceleration. Conversely, when the mass of an object rises, its acceleration decreases proportionally.

It is expressed mathematically as follows:

F=m⋅a

Where

F is the force applied to an object,
m is the mass of the object, and
a is the resulting acceleration.

This equation signifies that the force exerted on an object is directly proportional to both its mass and the acceleration it experiences. In simpler terms, applying force to an object will cause it to accelerate, with the acceleration being greater for objects with lower mass and vice versa.

Driving Newton’s Second Law

Force= Change of momentum with change of time

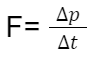
p=mv

Difference Form:

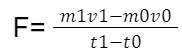
For constant mass:

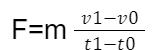
Force= mass*acceleration

For Changing mass:

Consider a scenario where we have a car positioned at point (0), denoted by location [math]X_0[/math] and time [math]t_0[/math]. The car possesses an initial mass [math]m_0[/math] and is in motion with a velocity [math]v_0[/math]. Upon being subjected to a force F, the car undergoes a transition to point 1, defined by location [math]X_1[/math] and time [math]t_1[/math].Consequently, the mass and velocity of the car transform to new values [math]m_1[/math] and [math]v_1[/math]. Newton’s second law becomes instrumental in determining these new values when the acting force is known.

By computing the difference between point 1 and point 0, an equation can be formulated to represent the force acting on the car:

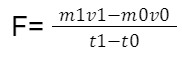
Let's assume the mass to be constant, a reasonable assumption for a car where the primary change in mass arises from the fuel burned between points "1" and "0." The weight of the consumed fuel is typically negligible compared to the overall mass of the car, especially when considering small increments in time.

For Constant mass

In the case of a constant mass, Newton’s second law can be expressed as:

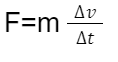
Considering that acceleration is defined as the change in velocity divided by the change in time, the second law can be simplified to a more recognizable form:

F=m⋅a

This equation states that an object will undergo acceleration when subjected to an external force.

Examples of Newton's Second Law

Pushing a Car:

Imagine trying to push a car. The force exerted is directly proportional to the mass of the car. A smaller car may be easier to accelerate, while a larger, heavier car will require a greater force to achieve the same acceleration.

Launching a Rocket:

In space exploration, when a rocket is launched, the force generated by the propulsion system is applied to the rocket's mass. As the mass of the rocket decreases (due to fuel consumption), the acceleration increases, adhering to Newton's second law.

Newton's Second Law in Problem Solving

Problem 1:

An object with a mass of 5 kg experiences a force of 10 N. Determine the acceleration of the object.

Solution:

Using Newton's second law equationF=m⋅a, we can rearrange it to solve for acceleration (a):

Substitute the given values:

Therefore, the acceleration of the object is 2 m/[math]s*2[/math]

Problem 2:

A force of 15 N is applied to an object, resulting in an acceleration of 3 m/[math]s*2[/math]. Determine the mass of the object.

Solution:

Rearranging Newton's second law equation to solve for mass (m):

Substitute the given values:

Therefore, the mass of the object is 5 kg.

Summary

Newton’s second law states that the force exerted on an object is directly proportional to both its mass and the acceleration it experiences.
An increase in the applied force results in a proportional increase in the object's acceleration.
Conversely, when the mass of an object rises, its acceleration decreases proportionally.
The force acting on the pendulum bob is proportional to its mass, determining the acceleration as it swings back and forth.

Related Worksheets: