The Work-Energy Theorem in Mechanical Systems

View Assign Share Link Report

The Work-Energy Theorem in Mechanical Systems

This lesson aligns with NGSS PS3.B

Introduction

The work-energy theorem is a fundamental principle in physics, forming the foundation of classical mechanics. It connects the concept of work done by forces to the energy changes within a system, such as lifting objects or accelerating masses. The theorem simplifies the analysis of forces and energy, offering an intuitive way to predict changes in kinetic and potential energy. In this article, we will explore the work-energy theorem, its mathematical formulation, and how it applies to various mechanical systems.

The Work-Energy Theorem Explained

The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy. In mathematical terms, this is expressed as:

$W_(n et) =DeltaKE$

Where:

$W_ (n et$ is the total work done on the object,
ΔKE represents the change in kinetic energy.
Work is the process by which a force applied to an object causes displacement, and it is mathematically described by:

$W = F.d costheta$

Where

W is the work done,
F is the magnitude of the force applied,
d is the displacement of the object,
θ is the angle between the force and the displacement.

The work-energy theorem implies that the work done on an object leads to a corresponding change in its kinetic energy. Positive work increases kinetic energy, while negative work (such as friction or braking forces) decreases it.

Application of the Work-Energy Theorem: Lifting Objects

When an object is lifted against gravity, work is done to increase its gravitational potential energy (GPE).

$PE= mgh$

Consider the case of lifting an object vertically from the ground. The force required to lift the object is equal to its weight, which is

$F=mg$ . The work done in lifting the object to height h is given by:

$F=m.d=mgh$

This work done against gravity is stored as gravitational potential energy. For example, lifting a 15 kg box to a height of 3 meters requires:

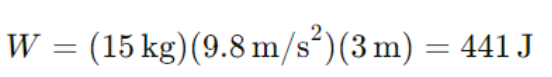
This 441 joules of work results in an increase in the box’s gravitational potential energy. If the box is subsequently dropped, this potential energy will convert back into kinetic energy as it falls.

Accelerating Masses: Kinetic Energy and Work

When a force is applied to an object, it causes the object to accelerate, resulting in a change in its velocity and, consequently, its kinetic energy.

Suppose a car of mass m starts from rest and accelerates under the influence of a constant force F. The car travels a distance d, and its final velocity is v. According to the work-energy theorem, the net work done on the car equals the change in its kinetic energy:

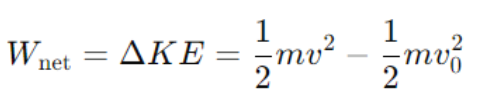
Where

$v_0$ is the initial velocity (zero in this case), and v is the final velocity.

For example, if a car with a mass of 1200 kg accelerates from rest to 25 m/s, the work done on the car is:

Thus, 375,000 joules of work are required to accelerate the car to this speed.

Work-Energy Theorem and Springs

The work-energy theorem is also applicable to systems that involve elastic potential energy, such as springs. Hooke’s law governs the behavior of springs, which states that the force exerted by a spring is proportional to its displacement from the equilibrium position:

$F=-kx$

Where:

k is the spring constant, which measures the stiffness of the spring,
x is the displacement from the spring’s equilibrium position.

The potential energy stored in a compressed or stretched spring is:

When the spring is released, the potential energy is converted into kinetic energy. The work-energy theorem can be applied to calculate how much energy is stored in the spring and how that energy is transferred to the object connected to the spring. For instance, if a spring with a constant k=200 N/m is compressed by 0.5 meters, the stored potential energy is:

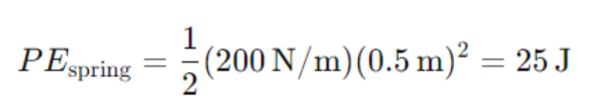
When released, this 25 joules of potential energy will be converted into kinetic energy, propelling the object attached to the spring.

Energy Dissipation and Non-Conservative Forces

In real-world mechanical systems, non-conservative forces such as friction and air resistance dissipate mechanical energy. The work-energy theorem can be extended to account for these energy losses by introducing a work term that represents the energy dissipated by non-conservative forces:

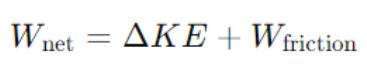
For instance, if friction slows down a car, the energy lost due to friction reduces the car’s kinetic energy, causing it to decelerate. Engineers use the work-energy theorem to account for these energy losses when designing systems like brakes, bearings, and gears, ensuring that the system operates efficiently even with energy dissipation.

Conclusion

The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy.
The work-energy theorem implies that the work done on an object leads to a corresponding change in its kinetic energy.
In real-world mechanical systems, non-conservative forces such as friction and air resistance dissipate mechanical energy.

Related Worksheets: